If you have read the coin game post (in case you haven’t, click here, read it - it is a quick and good read by the way -, and come back), you may wonder why the batch size of 6 produced the shortest completion time in the example game. Let’s find out. If we have a look at the flow of the game, we can find two major components: turning over the coins and moving them around (transfer). If you think about it, the time the players need to turn over all the coins is almost the same in each round. This action is so simple and we get so used to it that improving it during the game - in the given time frame - is nearly impossible. So, it is safe to state that the time spent on this component is constant during the game. However, if it is the case that the group finishes one round in 1 minute and 10 seconds, and another in 1 minute and 40 seconds, the variable must be the other component, which is the transfer time. It seems that there is a connection between the batch size and the time we need to move the batches around. Fortunately, Donald G. Reinertsen can explain this connection, and show us why the batch size of 6 produced the shortest transfer time and not 1 or 50.
He explains this phenomenon in his book The Principles of Product Development Flow with the U-Curve, but before getting into that, let me go back to the analysis of the turnover time and transfer time components for a while. If you have a bit closer look at the flow of the game, you’ll see three important things, not just two: the time required to turn over the coins, the time required to move the coins (both unturned and overturned), and the time a coin needs to go through all the players (lead time). I’ve already talked about the turnover part, so let’s focus on the other two. Similarly to the turnover action, I don’t see if one can improve the moving action significantly during the game. It is a simple straightforward thing: pick up the coins, push them or pull them. That is it. However, the batch size determines how often one should perform this action and that is not constant at all. The effort of picking and moving the coins multiplied by the frequency gives the transaction cost that actually depends on the size of the batch.
The last thing is the lead time. It has two parts: a turnover part and a waiting part. Let’s say that a player is turning over one coin and has one coin waiting. A coin is said to be waiting when the player is in possession that coin, but is turning over other coins. The wait can happen after the turnover or before depending on the group’s strategy (pull or push). The longer the waiting time, the longer the lead time. The connection between the size of the batch and the waiting time is linear: for a batch size of 10 the next batch has to wait 10 times as long as the time a player needs to turn over a coin. For a batch size of 5, it is only 5 times as long. This waiting has a certain cost to the group - longer overall completion time - , and it is called inventory or holding cost.
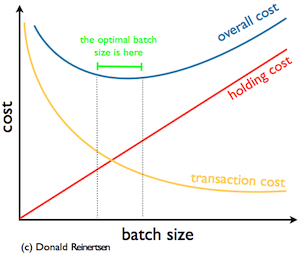Don Reinertsen’s genius was to realize that there was a connection between the transaction and holding costs. Have a look at the diagram on the right. You can see how the transaction cost changes by the size of the batch. The more items I transfer at once the lower the overall transaction cost is. On the other hand, the more items I have in a batch the larger my inventories are, which increases the holding cost. The optimal batch size is at the minimum of the aggregation of transformation and holding costs. The aggregated values form a kind of U-shape, hence the name: U-Curve optimisation.
Here is an example: let’s say I’m using wood for heating my house. If I buy all the wood at once for the whole heating season, my transaction cost will be low, because I have to pay the cost of the fuel and time only once, but I’ll need a place where I can store that huge amount of wood. So I have to build and maintain a storage shed, therefore the holding cost will be high. On the other hand, if I’m taking as much wood as I can use - let’s say - in two days, the holding costs are going to be low, but the transaction costs manifested in fuel and time are going be high. In order to reduce cost I have to find the optimal batch size. There is an important lesson here: the smallest batch size is not always the best batch size. We tend to forget about the transaction and holding costs, but it can hurt our business.
Let’s get back to the coin game. Unfortunately, I don’t recall all the details about the example game, and therefore I’m unable to show you how to calculate the optimal batch size for that particular game, but here is another example:
The calculation is not that straightforward in software development, but remember: the group that played the coin came had no idea about the optimal batch size concept, and still managed to find it by experimenting. Nevertheless, the idea that the transformation and holding costs can help you find the optimal batch size is extremely helpful. For example: the smaller the batches, the more frequently you have to run your test cases, but you have to do less merging: high transaction cost, low holding cost. While increasing the batch size the test running time decreases, but the merge time increases. The task is given: find the batch size that produces the optimal test running and merging times.
comments powered by Disqus